Die Hill-Chiffre basiert auf der Verwendung linearer Algebra.
Um eine Nachricht zu verschlüsseln, wird diese zuerst in Blöcke mit n Buchstaben aufgeteilt und jeder Buchstabe in eine Zahl umcodiert, wobei A=0, B=1, C=2, ... Y=24, Z=25 (Groß- und Kleinbuchstaben werden gleichermaßen behandelt).
Die Verschlüsselung geschieht nun durch Multiplizieren der Zahlen mit einer n x n Schlüsselmatrix modulo 26 (sofern A-Z das gewählte Alphabet ist). Das Ergebnis wird zurück in Text umgewandelt, wodurch der Ciphertext entsteht.

Sei die zu verschlüsselnde Nachricht: „ACT“ und der Schlüssel „GYBNQKURP“.¹
Da G=6, Y= 24, B=1 usw. ergibt sich für den Schlüssel die Matrix:

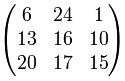
Die Nachricht wird zu diesem Vektor codiert:

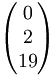
Zur Verschlüsselung werden Schlüssel und Nachricht miteinander multipliziert und der Ergebnisvektor modulo 26 berechnet:

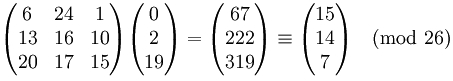
Dieses Ergebnis (15, 14, 7) kann dann wieder zu „POH“ codiert werden und ist somit das Ergebnis der Chiffrierung.
Zum Dechiffrieren wird der Chiffretext mit der inversen Matrix des Schlüssels multipliziert und der Ergebnisvektor modulo 26 berechnet.

Details:

Bei der Wahl des Schlüssels muss darauf geachtet werden, dass es eine inverse Matrix zu der Schlüsselmatrix gibt, damit die Nachricht wieder dechiffriert werden kann. Dazu muss die Determinante der Matrix modulo 26, teilerfremd zu 26 sein. Teilerfremde Zahlen von 26 sind: 1,3,5,7,9,11,15,17,19,21,23,25. Die Determinante der oben genannten Schlüsselmatrix berechnet sich:

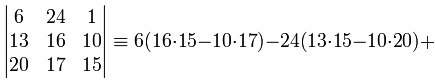
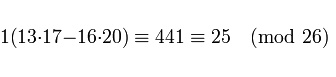
Manche Implementierungen wie http://massey.limfinity.com/207/hillcipher.php erlauben ausschließlich Primzahlen als modulo-Werte. Das führt generell zu einer höheren Sicherheit, allerdings ist es keine Voraussetzung der originalen Hill-Chiffre. Wenn z.B. eine Länge von 26 gewählt wird, meldet die Website, dass der Schlüssel nicht gültig ist, da die Alphabetlänge prim sein muss. Diese zusätzliche Voraussetzung kann beispielsweise durch das Hinzufügen eines Unterstrichs als erstes Alphabetelement erfüllt werden.
Implementierungen ohne diese Bedingung und mit der Möglichkeit, eine Schlüsselmatrix mit n>3 zu wählen, sind: CrypTool 1, CrypTool 2 oder SageMath.

Die Hill-Chiffre wurde 1929 von Lester S. Hill (*1891; † 1961) entwickelt, der die Methode in der Fachzeitschrift American Mathematical Monthly (Ausgabe 36) veröffentlichte.¹
Es stellt ein Blockchiffre dar, bei dem Buchstabengruppen gemeinsam durch eine Matrix verschlüsselt werden.

(1) de.wikipedia.org/wiki/Hill-Chiffre

Die Chiffre basiert ausschließlich auf linearer Algebra. Ist ein Teil des Klartextes bekannt, so kann ein lineares Gleichungssystem aufgestellt werden, um den Schlüsselsatz zu ermitteln.
Das beudeutet, dass die Hill-Chiffre anfällig für Known-Plaintext-Angriffe ist. Ein Angreifer, der n² Zeichenpaare abfängt, kann damit ein lineares Gleichungssystem aufstellen, welches grundsätzlich einfach lösbar ist.